法政大学国際文化学部

情報システム概論

担当　重定　如彦

2008年9月30日

 

第２回　データの表現

1.      データの表現

コンピュータは数字を計算するだけでなく、ワープロによって文字を、画像編集ソフトによって画像を、音楽ソフトによって音を、といったようにありとあらゆるデータを扱うことができます。コンピュータを使えば、様々な複雑な計算を行えるということは直感的にわかると思いますが、それでは計算と直接関係ないように見えるワープロによる文章編集や画像編集ソフトによる画像編集を一体どのようにしてコンピュータは行なっているのでしょうか？これを理解するためには、コンピュータがどのようにデータを表現しているかを学ぶ必要があります。

·           情報の符号化（または、コード化）

　コンピュータでは、あらゆるデータを数字に符号化して表現します。符号化とは、ある情報を数字や記号などの別の形に置き換えるということです。例えば我々は日常で「パーソナルコンピュータ」のことを「パソコン」、「アメリカ合衆国」のことを「米国」、「Operating System」のことを「OS」のように略して呼びますが、これらはまさに情報の符号化の例です。コンピュータが最も得意とするのは数字を扱うことです。そこで、コンピュータの世界では、あらゆる情報を数字に置き換える（符号化する）ことで表現します。

·           情報の最小単位「ビット」と２進数

コンピュータが情報を数字で表現すると述べましたが、コンピュータは我々が日常で使用する１０進数を使っていません。１０進数では０から９までの１０種類の数字を使って数を表しているのですが、１０進数をコンピュータが扱う情報の単位としてしまうと非常に面倒なことになってしまうからです。何故なら、コンピュータは電気を使って動いているのですが、電気を使って１０進数を表そうとすると例えば、１Vの電圧がかかっていたら１、２Vの電圧がかかっていたら２…のように電圧（または電流など）によって表さなければなりません。しかし、この方法では、１０種類もの電圧を区別する為の装置が必要になってしまい、装置が大変複雑になってしまいます。また、何らかの原因で２Vだったはずの電圧が１．５Vになってしまった場合などで、簡単に誤動作を起こしてしまいます。

そこで、コンピュータでは情報の単位として２進数を使っています。２進数では、　　　０と１の２種類の数字だけを使ってデータを表します。これを別のいいかたで言うと、　　０が「ない」、１が「ある」ということです。この「ある」と「ない」は情報の最小の単位であり、これを「ビット」と呼びます。電流が流れていない状態を「０」、流れている状態を「１」とすることで、１０進数と比べて複雑な回路を必要とせず、簡単にこの２進数を扱うことができるため、コンピュータでは数を２進数で表現します。

余談ですが、このビットを使えば世の中のあらゆるデータを表現することができるということを発見したのはクロード・シャノンという数学者です。

·           ２進数と１０進数

２進数と１０進数では、２進数のほうが表現できる数が少ないと思う方がいるかもしれませんが、２進数と１０進数は同等の表現力を持ちます。従って、１０進数で表現される数字を２進数に変換することができますし、またその逆も可能です。１０進数では数字の位が一つ上がるごとに、１の位、１０の位、１００の位…のように、桁が表す数字が１０倍になっていきますが、２進数の場合は１の位、２の位、４の位…のように２倍になっていきます。従って例えば　１１０１１　という２進数は

１＊１６　＋　１＊８　＋　０＊４　＋　１＊２　＋　１＊１　＝　２７

という計算により１０進数では２７であることが計算できます。

小数点以下の計算も同様です。２進数では、小数点以下の桁は、１／２の位、１／４の位、１／８の位…のように１／２倍となります。例えば　１１０１１．１０１　という２進数の小数点以下の部分は

１／２　＋　０／４　＋　１／８　＝　０．６２５　

となり、あわせて１１０１１．１０１という２進数は２７．６２５という１０進数と等しいということになります。

一方、１０進数を２進数に変換するには、整数部と小数点以下の部分を分けて計算します。整数部では、１０進数を２で割っていき、余りを順番に並べるという方法が有効です。この方法で１００という１０進数を２進数に変換すると以下のようになります。

 

２で割った余り

割った結果

 

１００

０

５０

０

２５

１

１２

０

６

０

３

１

１

１

０

２で割った余り（表の網掛けの数字）を下から順に並べた「１１００１００」が２進数で１０進数の１００を表した数字になります。

小数点以下の部分は、順番に小数点以下の部分に毎回２を掛けていき、掛けた結果の整数部を順番に並べていきます。例えば、０．６２５を２進数に変換するには

整数部分

 

小数部分

 

←　答えが０になるまで、

小数点以下の部分だけ

毎回２を掛けていく

０

．

６２５

１

．

２５

０

．

５

１

．

０

上記の整数部分を上殻から並べたもの、すなわち　０．１０１　が答えです。

なぜこの方法で１０進数を２進数に変換できるかを説明します。まず、１０進数のそれぞれの桁の数字を求める計算方法を考えて見ましょう。例えば　１２３４５．６７８　という１０進数の各桁の値は以下の方法で求めることができます。

 

整数部の各桁の求め方：

一の位：　１２３４５は以下のような式で表すことができます。

12345 = 1 * 10000 + 2 * 1000 + 3 * 100 + 4 * 10 + 5

 　　　　　          = (1 * 1000 + 2 * 100 + 3 * 10 + 4) * 10 + 5

　　　　　　この式から１２３４５の１の位は１２３４５を１０で割った余りで
求められることがわかります。

十の位：　先ほどの式の（）の中式に注目して下さい。（）の数字は１２３４５を１０で割った商です。この式は先ほどと同様に以下のように直すことができます。

  1 * 1000 + 2 * 100 + 3 * 10 + 4 = (1 * 100 + 2 * 10 + 3) * 10 + 4

                  従って、１２３４５の十の位は１２３４５を１０で割った商を、１０で割った余りで求められることがわかります。

百の位：　百の位以降も同様で、１２３４５を１０でどんどん割っていきその商を１０で割った余りを計算すれば求められます。

　この手順は２進数の場合でも全く同じです。先ほど説明した１０進数の整数部分を２進数に変換する手順が上記の方法と同じであることを確認して下さい。


練習問題：　１０進数の小数部を先ほど説明した方法で何故２進数に置き換えられるかを考えてみて下さい。基本的な考え方は、整数部の変換と同じです。

·           ８進数と１６進数とバイト

２進数はどうしても桁数が多くなってしまい、人間が扱うには不便な場合があります。そこで、２進数を３桁分（すなわち３ビット）まとめて０から７までの８種類の数字で数を表す８進数や、２進数を４桁分（すなわち４ビット）まとめて０から１５までの１６種類の数字で数を表す１６進数がよく使われます。１６進数の場合、０〜９までは１０進数と同じですが、１０〜１５までの数字は１０進数には存在しないので、１０から１５をそれぞれA、B、C、D、E、Fのアルファベットで置き換えて表現します。以下に１０進数で1から１６までの数字を２進数、８進数、１６進数に置き換えた表を挙げておきます。

数字を１０進数以外で表現した場合、何進数で表現しているかを示すために数字を括弧で括って括弧の右に小さく数字を書くことがあります。たとえば８進数の１５は（１５）　と記述します。なお、８進数や１６進数は人間が扱いやすいように２進数を置き換えたものです。実際のコンピュータの中では２進数が使われている点に注意して下さい。

 

2進数

8進数

10進数

16進数

 

2進数

8進数

10進数

16進数

1

1

1

1

 

1001

11

9

9

10

2

2

2

 

1010

12

10

A

11

3

3

3

 

1011

13

11

B

100

4

4

4

 

1100

14

12

C

101

5

5

5

 

1101

15

13

D

110

6

6

6

 

1110

16

14

E

111

7

7

7

 

1111

17

15

F

1000

10

8

8

 

10000

20

16

10

コンピュータではしばしば８ビットの数を一まとめにして扱います。この８ビットの数を１バイトと呼びます。ｎビットの数は２のｎ乗の数を表現することができるので、１バイトでは２の８乗、すなわち２５６種類の数字（０〜２５５）を表現することができます。また、１バイトの数字は２桁の１６進数で表現されることが多いようです。

·           文字データの表現

　それでは、コンピュータが２進数を使ってどのように様々なデータを符号化するか具体例をあげてみてみましょう。最初に文字データの符号化について述べます。コンピュータで表現できる文字はすべて数字で符号化されています。文字と数字を対応させた表を文字コード表と呼びます。最もよく使われる文字コード表としてはアルファベットと数字と記号を扱うASCIIコードがあります。ASCIIコードでは、一つの文字を7ビットのデータで表現し、１６進数で２０〜７Eのそれぞれの数字に文字が割り当てられています。なお、００〜１Fと７Fには文字ではなく、コンピュータを制御するための制御コードと呼ばれるものが割り当てられています（下の表では省略しました）。

ASCIIコード表（２０はスペース（空白）記号）

 

0

1

2

3

4

5

6

7

8

9

A

B

C

D

E

F

2

 

!

“

#

$

%

&

‘

)

(

*

+

,

-

.

/

3

0

1

2

3

4

5

6

7

8

9

:

;

< 

=

> 

?

4

@

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

5

P

Q

R

S

T

U

V

W

X

Y

Z

[

\

]

^

_

6

`

a

b

c

d

e

f

g

h

i

j

k

l

m

n

o

7

p

q

r

s

t

u

v

w

x

y

z

{

|

}

~

 

 

ASCIIコードでは一文字を一バイトの数値データで表現します。上記のASCIIコード表では、横が１６進数の下の桁、縦が１６進数の上の桁を表しています。例えば「ABC」という文字列は、ASCIIコードでは 41、42、43　という３バイトの１６進数で符号化されます。

数字とアルファベットを表現する他の有名な文字コードとしてEBCDICコードがあります。EBCDICコードはIBM社が自社のメインフレーム用に制定した文字コードで、パソコンではほとんど使われていませんが、メインフレームの世界では標準的に使われています。EBCDICの文字コード表は教科書の３４Pに記述されているのでそちらを参照して下さい。

一方、日本語はアルファベットと異なり文字数が非常に多く、１バイトの数字、すなわち０〜２５５の２５６種類のデータでは文字を表現しきれません。そこで、日本語を表現するために２バイト（＝１６ビット。０〜６５５３５までの６５５３６種類の数字を表現可能）のデータで表します。日本語を表す文字コードは実は１種類ではなく、よく使われるものだけでも、JIS、Shift-JIS、EUC、Unicode（ユニコード）の4種類あります。これらはそれぞれ、同じ数字でも割り当てられている文字が異なっている為、間違ってJISで書かれた文章をEUCだと思ってしまうと文章の意味がとおらなくなってしまします。ウェブブラウザなどで、時々文字化けが発生するのは、書かれている文章の文字コードをブラウザが勘違いしてしまうためにおこります。

 

·           数値データの表現

数字を表す場合、桁数に制限がなければあらゆる数を２進数で表すことができますが、実際にはコンピュータの記憶容量には限りがあります。そこでコンピュータでは、数字をどのように表現するかの形式をいくつか決めており、その形式に従って数字を表現しています。ここでは、実際に使われている数値データの表現方法についていくつか紹介します。

Ø  固定小数点数

　固定小数点数では一つの数字を一般に１６ビット（＝２バイト）又は３２ビット（＝４バイト）のデータで数を表現し、一番上のビットで符号（＋と−）を、残りのビットで数字を表現します。例えば、１６ビットの場合、一番上のビットで符号（０の場合は正の数、１の場合は負の数を表す）、残りの１５ビットで２進数の数を表現します。

１

０

１

１

０

０

０

０

０

０

１

１

１

０

０

１

符号

２進数の数字（１５桁）

 

例えば上記のデータは、符号の部分が１なので負の数、数字の部分が２進数で011000000111001（＝１０進数で１２３４５）なので、全体で −１２３４５ という１０進数を表します。１５ビットの２進数で２の１５乗＝３２７６８種類の数字を表現できるので、１６ビットの固定小数点表現では、−３２７６７〜３２７６７の範囲の整数を表現することができます。

固定小数点数では、小数点の位置が決められた位置（一番右端に小数点があるものとみなす）に固定されているため、基本的には整数しか表現できません。なお、固定小数点数には、上記の他にも、８ビットで数を表すものや、符合のないもの（正の数しか表現できない）など様々なバリエーションがあります。

Ø  浮動小数点数

固定小数点数では、小数点の位置があらかじめ固定されているため、小数点の位置がどこにあるかを示す必要はありませんでしたが、浮動小数点では小数点の位置が固定されていません。浮動小数点数では数字を数字の正負を表す「符号部」、小数点の位置を表す「指数部」、具体的な数字を表す「仮数部」の３つの部分で表現します。話をわかりやすくするために、10進数の浮動小数点数についてまず説明します。例えば、123.4567を浮動小数点数で表現すると

1.234567 *

のように、小数点が一番上の桁の次の位にある仮数部(1.234567)と、元の数字に直すために小数点を何桁ずらす必要があるかを表す指数部（)で表現します。指数部では、１０を何乗するかを示せば良いので、コンピュータ内部では123.4567を「1234567」と「2」の二つの数字で表現します。これに符号部を合わせたものが浮動小数点数です。

　浮動小数点数の利点は固定小数点数と比べて扱えるデータの範囲が広いことです。例えば、６つの１０進数の数字で数を表現する場合、固定小数点数では−999999〜999999の範囲の数字しか扱うことができませんが、６桁のうちの４桁を仮数部、２桁が指数部の浮動小数点数で表現したとすると、−9.999 *  〜 9.999 *  という実に膨大な範囲の数字を表現することができるのです。

浮動小数の欠点は、固定小数点数と比べると精度が低いことがあげられます。たとえば上記の例では固定小数点数では123456という数字を表現することができますが、浮動小数では、仮数部が４桁までしかないので、123400〜123499の間の数字を区別することができません。それ以外にも、小数点の計算を行わなければならないので浮動小数のほうが計算にかかる時間が長くなるという欠点もあります。

　上の例では10進数で説明しましたが、実際にはコンピュータは2進数でデータを扱っています。一般に使われている浮動小数点数には以下の２種類の形式があります。
　単精度浮動小数点数は4バイト（32ビット）で数字を表現し、32ビットのデータのうち1ビットを符号、23ビットを仮数部、8ビットを指数部に使用し、10進数になおすと、―3.40282 * 〜3.40282 * 　の範囲の値の数字を表現できます。倍精度浮動小数点数では倍の8バイトでデータを表し、　―1.79769 * 〜1.79769 * というとてつもない範囲の数字を扱うことができます。少しややこしいのですが、浮動小数点数では仮数部の数値は2進数の小数点以下の数値を表し、その値に1を足したものを実際の値として使用します。これは同じ数値を複数の方法で記述できないようにするためです。（前のページの10進数の数字を6個使った浮動小数点数の場合、100という数字を 0100 * 1000、0010 * 1001、0001 * 1002のように複数の方法で記述できてしまう）。
また指数部は単精度浮動小数点数の場合は実際には127を引いた値が使われます。

１ビット

８ビット

２３ビット

符号部

指数部

仮数部

短精度浮動小数点数の構成

（全体の長さは１＋８＋２３＝３２ビット＝４バイト）

例：　11000000111100000000000000000000 　を10進数に直す手順

仮数部
 
 

 


符号部が 1 なのでこの数値は負（マイナス）です。

指数部は10000001 （=10進数で129）となっていますが、実際にはこの値から127を引いた値が使われます。従って、指数部は129 −127 = 2 となります。
仮数部は111000000000000000000000 となっていますが、上で説明したとおり、この部分は小数点以下の部分をあらわし、その値に1を足したものが実際の指数部の数値になります。したがって、実際の指数部の値は 1.11100000000000000000000 となります。
これらのことから上記の数値は −1.111 * 22 ということになります。

* 22は、小数点の位置を右に2個ずらすという意味を持つのでこの数字は

2進数で −111.1 、すなわち10進数になおすと−7.5 となります。

Ø  ゾーン１０進数

　数字の各桁の数字を文字コードで表現します。例えば、１２３という数字をASCIIコードの場合、１６進数で３１、３２、３３と表現します（前述のASCIIコード表を参照して下さい）。ゾーン１０進数は文字コードをそのまま数に置き換えられるという利点がありますが、一桁の数字につき１バイトのデータが必要なので、数字のデータサイズが大きくなるという欠点があります。例えば固定小数点数では１バイトのデータで２の８乗＝２５６種類の数を表現できますが、ゾーン１０進数では０〜９までのたった１０種類の数しか表現できません。

Ø  パック１０進数

０〜９の数字は４ビットの２進数（０〜１５を表現できる）で表現可能です。そこで、４ビットの２進数を１０進数の一桁とみなして数字を格納するのがパック１０進数表現です。パック１０進数もゾーン１０進数と同様、数字データが１０進数を使って格納されているので、人間にとってわかりやすいという利点がありますが、本来ならば０〜１５の１６種類のデータを表現できる４ビットのデータを使って０〜９までの１０種類のデータしか使っていないので、データの表現の効率が悪いという欠点があります。

Ø  様々な数字の符号化の使い分け

固定小数点数や、浮動小数点数は数をコンピュータが実際に数字を扱う２進数で表現しているため、計算を高速に行うことができます。また、数のデータのうち全てのビットを利用するため、数を効率よく表現できるという利点があります。そのため、高速に大きな桁の計算が必要な場合に使われます。

１０進数と２進数の表現力は同じだと先ほど述べましたが、数を表現する時にビット数が限られている場合、１０進数と２進数を変換した場合に誤差がでる場合があります。例えば０．１という１０進数を２進数に変換してみて下さい。小数点以下の数が循環してしまうため、２進数では限られたビット数では０．１を表現できません。ゾーン１０進数やパック１０進数は計算速度やデータ表現の効率が悪いという欠点がありますが、１０進数の計算で誤差があってはならないような事務処理計算などで使われます。

·           デジタルデータとアナログデータ

コンピュータが扱うデータは文字データや数値データのようにすべて符号化（数値に変換）されたデータであり、このようなデータをデジタルデータと呼びます。これに対して、自然界にある音や色などのデータはアナログデータと呼びます。アナログデータとデジタルデータの違いは連続性にあります。アナログデータはデータに切れ目がありませんが、デジタルデータではデータを限られたビット数で表現しているため、例えば１６ビットの固定小数点数では整数しか表現できないように飛び飛びの値しか表現できないのです。

例えば人間の身長はアナログデータです。本当に正確に人間の身長を測ることが出来た場合、小数点以下に無限に数字が並ぶことになるでしょう。一方コンピュータの記憶容量は無限ではありませんので、このようなアナログデータを正確に扱うことはできません。そこで例えば身長の場合、小数点以下第２桁を四捨五入するといった方法を取ります。このようにコンピュータが扱うデジタルデータは、アナログデータの細かい部分を切り捨てて近似したデータです。コンピュータが扱うデジタルデータと実際のアナログデータの差を誤差と呼びます。誤差を小さくすればするほど、コンピュータが扱うデータのサイズが大きくなりますが、デジタルデータとアナログデータの見分けがつきにくくなります。

こうしてみると、アナログデータのほうがデジタルデータよりすぐれているように思えるかもしれませんが、アナログデータは劣化しやすいという欠点があります。例えばカセットテープレコーダーに録音された音はアナログデータで録音されている為、ダビングなどでコピーを行うたびに完全に正確なコピーが行えないためどんどん劣化していきます。また、声というアナログデータで人から人へ情報を伝えていくといういわゆる伝言ゲームを行うと大抵の場合途中で情報が劣化して最初の情報と異なってしまいます。

これに対し、紙に書かれた文字やCDに録音されている音楽データはデジタルでデータが記録されているため、コピーを行っても全てのデータを正確にコピーすることができます。CDをコピーした場合、何回コピーしても音質が劣化せず、元のCDと全く同じものをコピーすることができるのはデータがデジタルデータで保存されているからなのです。

·           音の表現

　次はコンピュータが音をどのようにしてデジタルデータに符号化するかについて説明します。音は波でできており、次の図のａのように波線で表すことができます。

コンピュータはこれをサンプリングと呼ばれる方法でデジタル化します。サンプリングでは、まず時間を非常に細かく区切ってそれぞれの時間毎に音の強さを記録してゆきます。この区切る時間のことをサンプリング周期と呼び、サンプリング周期を短くすればするほど正確な音を表現することができます。次にサンプリング周期で区切られた時間毎の音の振幅を記録するのですが、この時の区切りの幅を量子化レベルと呼び、区切り幅を狭くすればするほど、振幅をより細かく正確に記録することができます。区切り幅を２進数に変換したときに必要なビット数のことを量子化ビットと呼びます。

 

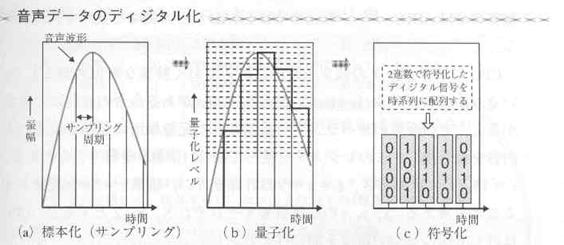
図のａように、元のアナログデータである音は滑らかな曲線で表現されますが、コンピュータではこれをサンプリングによって図のｂのようにギザギザの折れ線に変換し、それを図のｃのように２進数に置き換えることでデジタル化します。こんな方法では、元の音データとは違うものが録音されてしまうのではないかと心配される方もいると思いますが、区切る時間を非常に細かくすることで現在の技術では元の音とコンピュータが記録したデータを人間の耳が聞き分けられることができないレベルまで達しています。例えば、CDはサンプリング周期が44100Hz (ヘルツ)、量子化ビットが１６ビットで音をデジタル化しています。これは、1/44100秒に一回、音の振幅を１６ビットのデータ、すなわち２の１６乗＝６５５３６種類の数で表現していることを意味します。余談ですが音をCDなどに録音するときに使われるA/D変換という単語は「Analogue To Digital Conversion」、（アナログからデジタルへの変換）の略です。

 

·           画像の表現

　世の中にある絵などの目で見ることのできる情報はすべてアナログデータです。コンピュータではこれらを２種類の方法で符号化して表現します。一つ目の方法は、色の符号化です。色は赤、青、緑の光の３原色と呼ばれる色を混ぜることで表現できます。コンピュータでは一つの色を表現する場合、この赤、青、緑の強さの度合いを数字に置き換えて表現しているのです。最近では赤、青、緑をそれぞれ０〜２５５の８ビットのデータで表現しており、３つあわせて２５６＊２５６＊２５６＝約１６７７万種類の色を表現することが可能です。実際にはさらに細かく色を表現することも技術的には可能なのですがこれ以上色数を増やしても人間の目には区別できないということでこの数になっているようです。

 

色のデジタル化（各色を０〜１００で表現した場合）

赤

緑

青

色

100

0

0

赤

50

0

0

暗い赤

0

0

0

黒

100

0

100

紫

100

100

100

白

 

　もう一つの方法は、色の範囲を小さな正方形の点で表現するという方法です。コンピュータのディスプレイをよくみてみると、ディスプレイ上に表示されている文字や画像がすべて点の集まりで表現できていることがわかると思います。この一つ一つの点には先ほどのべた色が符号化された数値で表現されており、この点が集まって画像になっています。例えば「Ａ」という文字を画像で表現する場合、以下のような７＊５のサイズの各点に白と黒の色を割り当てることで表現することができます。

 

 

 

 

 

 

黒

 

 

 

黒

 

黒

 

黒

 

 

 

黒

黒

黒

黒

黒

黒

黒

 

 

 

黒

黒

 

 

 

黒

黒

 

 

 

黒

 

 

 

 

 

 

 

 

この点を細かくすれば細かくするほど、画像データをより正確に表現することができます。コンピュータのディスプレイの中の点の横と縦の数を解像度と呼び、昔のコンピュータのディスプレイの解像度は６４０＊４８０で、一つの点の色を１バイトのデータで表現していました。１バイトのデータでは色をたった２５６種類しか表現できないため、昔のコンピュータでは写真のような綺麗な画像を表現することは不可能でした。一方、最近のコンピュータでは技術の発達により、１０２４＊７６８、１６００＊１２００といった高い解像度で一つの点を４バイトのデータで表現することができるようになっており、写真のような細かく綺麗な画像を表現することができるようになっています。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.      課題

以下の問題を解き、ta080017@mail.edu.i.hosei.ac.jpに課題のメールとして送って下さい。解答はメール本文に直接書くか、Wordやメモ帳などに書いて添付ファイルとして送って下さい。締切りは来週の授業までです。なお、計算が必要な問題は、答えだけでなく計算の過程も書いて下さい。なお、計算の際に電卓を使ってもかまわないことにします。

 

1.         ７５３．６８７５　という１０進数を２進数に直せ。

2.         １０１１０．０１１　という２進数を１０進数に直せ。

3.         ８４　という１６進数を１０進数に直せ。

4.         −２００３　という１０進数を１６ビットの固定小数点数で表現するとどうなるかを計算せよ。答えは例えば　０１１００１００１０１０１０００　のように１６個の０と１で記述すること。

5.         −１０１１０．０１１　という２進数を単精度浮動小数点数で表現するとどうなるかを計算せよ。答えは問４と同様の形式で３２個の０と１で記述すること

6.         Ｉ　ａｍ　ｈａｐｐｙ．　という文章はASCII コードでどう表現されるかを述べよ。答えは１６進数の数字を「、」で区切って書くこと。注：空白は１６進数で２０である。
答えの例　３１、３２、３３

7.         ＣＤ（サンプリング周期が44100Hz、量子化ビットが１６ビット（＝２バイト））で２分間音楽を録音した場合、何バイトのデータになるか計算せよ。

8.         １０２４＊７６８のサイズで、一つの点の色を４バイトのデータで表現した場合、画像全体で何バイトのデータになるか計算せよ。

 

 

 

 

 

 

 

 

 

 

 

出席のメールはta080017@mail.edu.i.hosei.ac.jpにお願いします。

質問のメールなどは、sigesada@hosei.ac.jpまでお願いします。

授業の資料の最新版はhttp://www.edu.i.hosei.ac.jp/~sigesada/にあります。